10.5. Смешанные стратегии и их свойства

 

Пример 10.4.  Задержание подозреваемого.

Рассмотрим дилемму оперативного работника, направляющегося на задержание подозреваемого, с точки зрения теории игр. Опишем конфликтную ситуацию, несколько упростив ее. Оперуполномоченный может пойти на задержание один, а может вызвать группу захвата. Его противник, предварительного не зная  о силах и средствах милиции, в свою очередь, может оказывать или не оказывать сопротивление представителям правоохранительных органов.

Вариант, при котором оперативник пойдет один и своими силами сможет задержать преступника, оценивается им как выигрыш в 3 единицы (очень хорошо). Также оценивается и тот случай, когда преступник окажет сопротивление и решение вызова группы захвата окажется вполне своевременным. Если оперативник предпримет попытку задержания в одиночку, не расчитав свои силы, и данная попытка не увенчается успехом ввиду сопротивления задерживаемого, то оперуполномоченный проигрывает 1 единицу. Т.е. его выигрыш составит –1. При неэффективном вызове группы захвата оперативник выигрывает всего 1 единицу.

Заметим, что введенные платежи, на основании которых будет получено решение конфликта, оценены нами достаточно условно. При описании конкретного случая нужно стремится задать их, обосновывая количественно, к примеру, с помощью теории вероятностей. Теория игр на этот счет никаких рецептов не дает. Она может лишь сказать, как поступить в случае с уже заданной платежной матрицей, чтобы выиграть как можно больше или проиграть как можно меньше вне зависимости от действий противника.

Платежная матрица в этом случае будет такова:

.

Наибольшее значение минимумов строк равно 1. Это соответствует второй стратегии оперативника. Наименьшее значение максимумов столбцов – 3 (впрочем, максимумы столбцов в этой матрице совпадают). Мы видим, что нижняя и верхняя цена игры не равны друг другу. Значит, платежная матрица не имеет седловую точку и конфликт не может быть разрешен в чистых стратегиях. Рассмотренный выше способ решения игры уже не применим. Если оперуполномоченный применит вторую стратегию, то это гарантирует ему выигрыш в 1 единицу. Но взять эту стратегию в качестве чистой, т.е. всякий раз при задержании подозреваемого вызывать группу захвата, было бы, безусловно, неэффективно. Это означало бы «стрельбу из пушки по воробьям». Как интуитивно понятно, оперативник должен применять обе стратегии в зависимости от предполагаемой ситуации. Естественно, что в каждом конкретном случае он реализует какую-то одну из них. И теория игр не дает рецепта по поводу того, как поступать оперативнику в отдельном случае. Она, как мы увидим дальше, лишь определяет вероятности применения стратегий игроками. Эти вероятности зависят от условий задачи, т.е. тех платежей, которые были заданы изначально.

 

Пример 10.5. Ещё одно задержание подозреваемого. В этом примере подозреваемый может находиться в двух местах А и В, известных оперуполномоченному, а оперативник пытается его задержать, направляясь в одно из них. Если оперуполномоченный направляется в то же место, где находится подозреваемый, то задерживает его. В этом случае его ход (стратегия) оценивается выигрышем +1. Если же оперативник выбирает место противоположное тому, где находится подозреваемый, то подозреваемый скрывается от правоохранительных органов. Выигрыш оперативника при этом составит  . Таким образом и у оперуполномоченного, и у подозреваемого есть две возможные стратегии. Оперативник может направиться в пункт А (1-я стратегия) или в пункт В (2-я стратегия). Подозреваемый, в свою очередь, независимо от решения противника, может находиться либо в А (1-я стратегия), либо в В (2-я стратегия).Из приведенного ниже рисунка найдём платёжную матрицу игры.

 

 Т.е. матрица платежей равна

.

Легко убедиться, что в данной матрице также нет седловой точки. Значит, и не существует одной чистой  стратегии игроков, это и понятно, т.к. у каждого игрока обе стратегии совершенно равноправны. При отсутствии дополнительных источников информации оперуполномоченный принимает любую свою стратегию с вероятностью . Если подобная ситуация повторяется неоднократно, то оперативник должен менять свои стратегии, чтобы преступник не разгадал его тактику. Т.е. он должен применять попеременно то одну, то другую стратегию. То же самое можно сказать и применительно к подозреваемому.

 

Пример 10.6. Просто платежная матрица. Для удобства рассуждения и выводов оторвемся от моделирования практических ситуаций юридической деятельности и рассмотрим некую прямоугольную игру с платежной матрицей:

.

В данной матрице нет седловой точки. Нижняя цена игры равна 2. Это соответствует 2-й стратегии первого игрока. Верхняя цена игры равна 3, что соответствует 1-й стратегии его противника. Это значит, что, применяя свою чистую стратегию, первый игрок может гарантировать себе выигрыш в 2 единицы. Второй игрок может быть уверен, что проиграет не более 3 единиц.

Однако, если первый будет все время применять вторую стратегию, то второй игрок, обнаружив это, будет также применять свою вторую стратегию и снизит свой проигрыш до 2. Если подобное повторится неоднократно, то первый игрок увидит, что ему выгодней применить первую стратегию и увеличить свой выигрыш до 4. В ответ на это второй может также поменять свою стратегию на первую и выигрыш первого тогда составит лишь 1 единицу. При первой же стратегии противника первому игроку желательно использовать вторую стратегию и выигрывать 3 единицы, и т.д.

Приведенное рассуждение отчетливо показывает, что в данной игре обоим игрокам невыгодно останавливаться на какой-то одной стратегии. Остается лишь одна альтернатива: каждый игрок должен применять обе стратегии. Естественно, что чаще всего совмещение стратегий в какой-либо отдельной партии невозможно (ниже мы рассмотрим пример, где оптимальным решением будет совмещение чистых стратегий). Поэтому и первый, и второй игрок должны применять попеременно то одну, то другую стратегию.

Оптимальной стратегией игроков будет сложная стратегия, содержащая в качестве своих элементов их чистые стратегии. Такая стратегия называется смешанной. Цена игры при применении оптимальной смешанной стратегии (т.е. тот наибольший выигрыш, который может гарантировать себе первый игрок, и тот наименьший проигрыш, который может обеспечить второй) лежит между нижней и верхней ценой игры. И чем больше разница между нижней и верхней ценой, тем больше эффективность применения смешанной стратегии по сравнению с чистой.

У каждого из игроков возникает вопрос: как часто необходимо применять первую стратегию и как часто вторую? Означает ли “попеременность” то, что при многократном повторении игры в половине партий нужно выбрать первую, а в половине – вторую стратегию?

Речь идет о нахождении относительных частот применения каждой стратегии для каждого игрока. В нашей игре 2´2 для установления смешанной стратегии первого игрока мы должны найти два числа  и , которые означают, что при количестве партий + в  партиях первый игрок должен следовать 1-й стратегии, а в  партиях – второй стратегии. (Для исследования игры полностью необходимо найти и относительные частоты стратегий второго игрока:  и .)

Частоты применения стратегий игроков записывают в виде отношения :, :.

Другая проблема для применения смешанной стратегии состоит в том, чтобы указать, в каких  партиях первый игрок должен выбирать стратегию 1, а в каких  партиях - стратегию 2. Ведь если противник узнает чередование стратегий, т.е. тактику, то он может извлечь для себя определенную выгоду. Значит, необходимо соблюдать меры по сохранению секретности: второй игрок не должен знать какую чистую стратегию предполагает применить первый в каждой отдельной будущей партии. Естественно, что предыдущие реализации решений уже известны обоим игрокам.

Существует метод, являющийся надежной защитой сохранения секретности выбора, основанный на самой природе игры. Он состоит в том, что решение относительно выбора стратегии принимается на основании подходящего случайного события (жребия). Случайный механизм является существенной частью оптимальной смешанной стратегии. При этом противник лишен возможности узнать наперед о важных действиях, потому что эти действия неизвестны и вам самим.

Может показаться, что случайный механизм выбора стратегии является безответственной операцией, особенно когда исход игры имеет важное значение. Однако в действительности это не так. Ведь все рассуждения и выводы, которые должны предшествовать принятию решения имеют здесь место. Случайный механизм появляется уже после того, как задача сформулирована, платежи назначены, подсчитаны относительные частоты, управляющие случайным механизмом и, следовательно, выбором стратегий. Значит случайный механизм – оружие вашей воли, а не ваш хозяин.

 

Если имеется только одна реализация игры, то более точнее будет говорить не об определении относительных частот стратегий, а о наборе вероятностей применения чистых стратегий. Отношение вероятностей стратегий равно отношению частот. Обозначим вероятности применения первой и второй стратегий первым игроком через  и . Тогда для  и  можно записать:

 ; ;  (эти вероятности составляют полный набор);

 .

То же самое можно записать и для вероятностей применения своих стратегий вторым игроком:  и .

; ;  (эти вероятности также составляют полный набор);

 .

Если найдены относительные частоты стратегий, то набор вероятностей найти достаточно легко:

;  ;    ;  .

Если же известен набор вероятностей , , то относительные частоты можно определить, умножив соответствующие вероятности на целое число, чтобы получившиеся частоты по возможности также были целыми. Действительно, набор относительных частот определен с точностью до множителя и набор частот 1 : 2 эквивалентен 2 : 4 или 4 : 8 или 8 : 16.

Итак, смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.

Если первый игрок имеет m чистых стратегий i = 1...m, то его смешанная стратегия определяется набором чисел :  (i = 1...m), .

Аналогично, смешанная стратегия второго игрока определяется набором вероятностей его n чистых стратегий: :  (j = 1...n), .

Если какая-либо вероятность из набора равна 0, то это означает, что соответствующая чистая стратегия не применяется в смешанной. Так, набор вероятностей ; 0;  означает, что первая и третья стратегии должны применяться с относительными частотами 1:3, а вторая стратегия вообще не используется.

Итак, нахождение смешанной стратегии противников в игре сводится к нахождению набора вероятностей их чистых стратегий или их относительных частот.

Вернемся к примеру 10.6. Пусть первый игрок выбирает первую стратегию с вероятностью x. Второй – свою первую стратегию с вероятностью y. Тогда выбор вторых стратегий определится как 1-x и 1-y соответственно для первого и второго игроков.

Рассмотрим математическое ожидание выигрыша первого игрока.

.

 

(Математическое ожидание выигрыша первого игрока в общем случае определяется так:

, где

 - набор вероятностей стратегий первого игрока,

 - набор вероятностей стратегий второго игрока,

 i=1…m,  j=1…n – платежная матрица игры.)

 

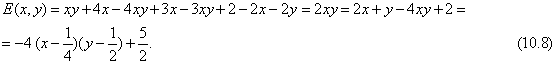
Можно показать, что точка  и  является седловой точкой для функции .  Значит, если первый игрок будет применять первую стратегию с вероятностью , а вторую  - с вероятностью , то математическое ожидание его выигрыша составит . Второй игрок должен применять и первую, и вторую свои стратегии с равными вероятностями - . Следовательно, можно сделать вывод, что оптимальная смешанная стратегия для первого игрока определяется набором вероятностей (;), а второго – (;). Очевидно, что  является ценой этой игры.

Оказывается, что исследование игр со смешанными стратегиями аналогично играм, имеющим седловые точки в чистых стратегиях. Но только если раньше анализировалась сама платежная матрица, то в этом, более общем случае нужно искать седловые точки для функции среднего выигрыша игроков – математического ожидания выигрыша.

         Средний выигрыш первого игрока в игре с платежной матрицей A выражается в виде математического ожидания его выигрышей:

,                                              (10.9)

где ,  - наборы вероятностей первого и второго игроков соответственно.

Первый игрок стремится за счет применения своих смешанных стратегий X максимально увеличить свой выигрыш, а второй, подбирая набор вероятностей Y, - сделать  как можно меньше.

Если смешанные стратегии , образуют седловую точку функции (10.9), т.е. для всех наборов вероятностей X и Y верно неравенство:

,

то они называются оптимальными смешанными стратегиями соответственно первого и второго игроков.

         В чем же смысл оптимальных смешанных стратегий? Применяя , первый игрок может гарантировать себе выигрыш не меньший  независимо от того, как поступит второй. Аналогично, используя , второй игрок не даст получить первому больше, чем . Итак, величина , называемая ценой игры, - это сумма, не меньше которой может получить первый игрок, выбирая , и не больше которой он получит, если второй игрок выберет .

         Величина  называется верхней ценой игры, а  - нижней ценой игры.

         Используя теорему 1 предыдущего параграфа, для оптимальных смешанных стратегий можно записать:

                  (10.10)

         Совокупность оптимальных смешанных стратегий ,  и цены игры  называется решением матричной игры.

 

         Теперь перед нами возникают два вопроса:

1.  Все ли матричные игры имеют решение в смешанных стратегиях?

2.  Как находить решение матричной игры?

Ответом на первый вопрос служит основная теорема матричных игр, впервые доказанная Джоном фон Нейманом.

 

Теорема 2.        Всякая матричная игра имеет цену. Игрок в матричной игре всегда имеет оптимальную стратегию.

 

         В терминах набора вероятностей стратегий и математического ожидания выигрыша первого игрока теорема 2 звучит так.

 

Теорема 3. Для любой матричной игры, определяемой платежной матрицей А, величины  и  существуют и равны между собой.

 

         То есть для любой матрицы будет выполняться равенство (10), которое и определяет цену игры v и оптимальные смешанные стратегии игроков , .

Для нахождения оптимальных смешанных стратегий и цены игры матрицы любой размерности приведем несколько теорем, описывающих свойства этих стратегий.

 

Теорема 4.  Для того чтобы в матричной игре с ценой игры v смешанная стратегия первого игрока  была оптимальной, необходимо и достаточно, чтобы для любой смешанной стратегии Y  второго игрока выполнялось неравенство:

.

 

Аналогично для второго игрока, чтобы смешанная стратегия  была оптимальной, необходимо и достаточно, чтобы для любой смешанной стратегии X первого игрока выполнялось неравенство .

 

Следствие из теоремы 4

         Для того чтобы  была оптимальной смешанной стратегией первого игрока матричной игры с матрицей А и ценой игры v, необходимо и достаточно, чтобы  для всех j (j=1…n) выполнялись неравенства:

.

         Аналогично для второго игрока: чтобы  была оптимальной смешанной стратегией второго игрока, необходимо и достаточно, чтобы для всех i (i=1…m) выполнялись следующие неравенства:

.

         Из этого следствия вытекает, что оптимальные смешанные стратегии и цена игры для матрицы любой размерности находятся из решения следующей системы неравенств и уравнений:

         Вышеизложенное следствие применимо также и в обратную сторону: если мы каким-либо образом установили предполагаемое решение игры, то неравенства следствия можно использовать для его проверки.

         Следующая теорема также оказывается полезна при решении некоторых матричных игр.

 

Теорема 5. Пусть имеется матричная игра с платежной матрицей А, ценой игры v и оптимальными смешанными стратегиями ,  первого и второго игроков соответственно. Тогда, если для некоторого i , то .

Если для некоторого j , то .

Оказывается, что нахождение решения игры уже с матрицей 3´3 представляется весьма сложной математической процедурой. Поэтому в нашем курсе ограничимся рассмотрением случая матриц размерностью 2´2.

Предыдущая | Главная | Глава 10 | Следующая