6.6            Нормальный закон распределения

 

Нормальный закон распределения играет в теории вероятностей особую роль. Он является наиболее часто встречающимся на практике законом распределения вероятностей. Нормальному распределению приближенно подчиняется сумма достаточно большого числа независимых случайных величин, описываемых какими угодно законами распределения. Приближение выполняется тем точнее, чем большее количество случайных величин суммируется. А большинство встречающихся на практике величин, таких, например, как ошибки измерений, ошибки стрельбы, могут быть представлены как суммы большого числа малых слагаемых – элементарных ошибок, каждая из которых вызвана отдельной независимой причиной. Особенности отдельных законов распределения нивелируются в общей сумме и эта сумма оказывается подчинена закону, близкому к нормальному. Главное, чтобы элементарные ошибки играли в общей сумме сравнительно малую роль.

Центральная предельная теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

 

Дадим определение нормального распределения случайной величины.

Говорят, что случайная величина Х распределена по нормальному закону с параметрами а и , если плотность распределения вероятностей имеет вид:

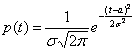, –¥<t<¥.

         Вероятностный смысл параметров а и  таков: а – математическое ожидание случайной величины Х, s – среднее квадратическое отклонение величины.

         Иногда такой закон распределения называют Гауссовским. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). На рис. 6.11 изображены нормальные кривые с параметрами а=1 и  , , .

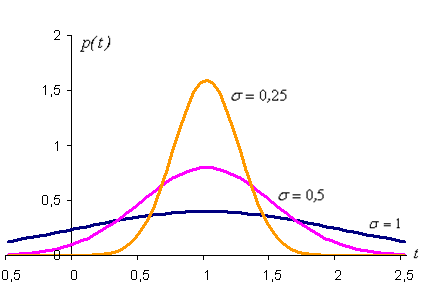
Рис. 6.11

 

         Из рис. 6.11 видно, что положение пика кривых определяется параметром а=1, а параметр s (среднее квадратическое отклонение) характеризует форму нормальной кривой. При увеличении s уменьшается максимум кривой распределения, сама кривая становится более пологой, растягиваясь вдоль оси абсцисс. И, наоборот, при уменьшении s  возрастает максимум кривой распределения, сама кривая становится более «островершинной». Площадь, ограниченная любой нормальной кривой и осью абсцисс, равна единице. Параметр а (математическое ожидание величины) определяет положение максимума на оси абсцисс, не влияя на форму кривой. На рис. 6.12 показаны нормальные кривые с одинаковым средним квадратическим отклонением  и разными математическими ожиданиями а=–1, а=0, а=1.

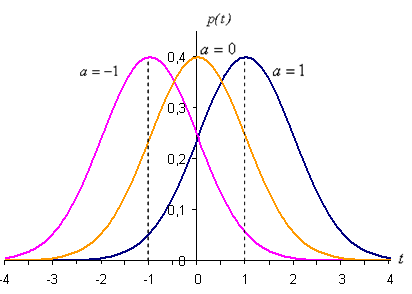
Рис. 6.12

        

         Нормальное распределение с параметрами а=0 и  называется нормированным. Плотность нормированного распределения

.

Значения этой функции на отрезке [0:3] с шагом 0,01 приведены в таблице Приложения 1. Нормированная нормальная кривая показана на рис. 6.11.

         Функция общего нормального распределения равна

=.

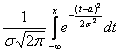         Функция нормированного нормального распределения

=.

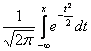         Можно показать связь между функциями  и :

=.

Для x>0 можно представить = + .

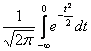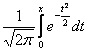Так как ==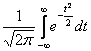1 и подынтегральная функция симметрична относительно нуля, то 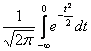=0,5.

         Тогда

=0,5 + Ф(х)    (x>0).

Функция Ф(х) называется функцией Лапласа:

Ф(х)= .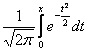

Значения функции Лапласа на отрезке [0:3]  с шагом 0,01 также приведены в таблице Приложения 1.

Из определения следует, что функция Лапласа является нечетной функцией

Ф(–х) = – Ф(х).

Для x<0 =0,5 – Ф(х).

Вероятность того, что случайная величина Х, распределенная по нормальному закону с параметрами а и , примет значение, принадлежащее интервалу (a, b), равна

P(<Х<) = F() – F() = –= –.  (6.9)

         Пример 6.14. Случайная величина Х распределена по нормальному закону с параметрами а =10 и =4. Найти вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале (8, 12).

         Используя формулу 6.9 и учитывая, что а =10 и , получим:

P(8<Х<12) =–=–.

         Так как = –, то P(8<Х<12)=2×.

         По таблице значений функции Лапласа находим Ф(1)=0,3413. И, следовательно, P(8<Х<12)=2×0,3413=0,6826.

         Вычислим вероятность того, что случайная величина принимает значения, отстоящие от ее математического ожидания а на величину не более, чем 3s, т.е. лежащие в интервале (а–3s, а+3s).

P(а–3s <Х< а+3s) =  –  = Ф(3) – Ф(–3) = 2×Ф(3) = 2×0,49865 = 0,9973.

         Таким образом, вероятность того, что абсолютная величина отклонения случайной величины будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Вероятность противоположного события – того, что отклонение по абсолютной величине превысит утроенное значение s – очень мала (равна 0,0027). Поэтому можно считать, что для нормально распределенной величины все значения (с точностью до долей процента) укладываются в интервале (а–3s, а+3s). Это утверждение носит название «правило трех сигм». Значит, зная математическое ожидание и среднее квадратическое отклонение случайной величины, можно ориентировочно указать интервал ее практически возможных значений. И наоборот, если известно максимально возможное отклонение случайной величины от среднего, то, поделив его на 3, можно оценить значение среднего квадратического отклонения.

Предыдущая | Главная | Глава 6 | Следующая