7.1. Основы математической статистики

 

Для эффективного функционирования органов внутренних дел требуется  качественная информация о состоянии преступности, которая должна определенным образом обрабатываться для получения выводов и рекомендаций. Социально-демографические, уголовно-правовые и иные характеристики лиц, совершивших преступление, носят случайный характер, а изучением закономерностей случайных процессов занимается математическая статистика. При изучении случайных процессов необходимо решить ряд задач. Первая такая задача заключается в нахождении приближенного выражения для функции распределения или плотности вероятности по эмпирическому материалу и в выводе способа получения нескольких рационально выбранных числовых характеристик всей совокупности этих характеристик, которые дали бы представление о всей совокупности. С этой задачей тесно связана вторая: найти вероятность того, что случайно выбранный объект совокупности имеет значение величины в заданных границах. Этими задачами можно было бы ограничиться, если бы эмпирическая совокупность содержала все объекты исследуемого типа; такие полные совокупности называют генеральными. Простейший пример генеральной совокупности - материалы переписи населения, в которых имеются сведения о всех гражданах. В обычных задачах известна совокупность, представляющая выборку существующей, генеральной совокупности, только часть которой удалось обнаружить наблюдениями. Если одни объекты генеральной совокупности чисто случайно попадают в результаты наблюдений, а другие не попадают, то мы имеем случайную выборку из генеральной совокупности. В целом ряде задач  объекты генеральной совокупности не все попадают в статистический материал не по случайным причинам, а потому, что нет возможности  выделить у них тот признак, по которому подобрана совокупность. В таких случаях говорят, что совокупность есть результат селекции.

Если для выборочной совокупности полностью решены первые две задачи, то возникает третья задача: выяснить, в какой мере полученные числовые параметры выборочной совокупности описывают генеральную совокупность.

Мы ограничимся рассмотрением вопроса о том, как разработать способы получения нескольких чисел, которые можно было бы считать достаточно полно описывающими данную статистическую совокупность.

До анализа  и интерпретации статистической информации, являющейся некоторой совокупностью количественных данных, обычно необходимо их обобщить. На начальном этапе данные представляют в виде несгруппированного ряда: осуществляется обычное упорядочивание количественных оценок от минимальной до максимальной  или наоборот. Следующий этап - распределение частот. Этот этап в большинстве задач можно пропустить и приступить  к представлению информации в виде сгруппированных частот.

Для этого определяется или выбирается число интервалов, в каждом из которых все попадающие в них значения наблюдений считаются равными друг другу.

Шаг интервала определяется из выражения:

,

где и - соответственно максимальное и минимальное значение измеряемой величины;

k - число интервалов.

Определив середины интервалов и взяв полученные значения в качестве вариант, получаем последовательность равноотстоящих вариант.

Для наглядности строят различные графики статистического распределения выборки, например полигон и гистограмму. Полигоном частот называют ломаную, отрезки которой соединяют значения вариант выборки на соответствующих им частотах.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы частот, а высоты определяются количеством значений измеряемой величины, попадающих в соответствующий интервал.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат интервалы частот, а высотой - частоты выпадения значений измеряемой величины в данном интервале частот.

Для анализа статистической информации используются следующие количественные характеристики: среднее арифметическое, среднее геометрическое, медиана, мода, дисперсия, среднее квадратическое отклонение. Такие статистические оценки называют точечными.

Среднее арифметическое определяется из выражения:

 ,

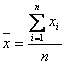где - значения наблюдений измеряемой величины,

- общее число наблюдений,

Среднее геометрическое (используется для изучения динамики явлений) определяется из выражения:

,

где - частоты выпадения измеряемой величины в соответствующем интервале,

.

Медианой   называют варианту, которая делит поровну вариационный ряд.

Модой называют варианту, которая имеет максимальную частоту в вариационном ряду.

Дисперсия измеряемой величины характеризует меру рассеяния результатов наблюдений относительно средневзвешенного и определяется по формуле:

.

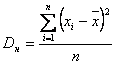При большом числе наблюдений  такая оценка дисперсии является состоятельной. При малом числе наблюдений - смещенной, т.к. ее математическое ожидание не равно дисперсии генеральной совокупности , а меньше  на . Для устранения смещенности  оценку дисперсии умножают на поправочный множитель Бесселя. Тогда выражение для дисперсии перепишется в виде:

 

.

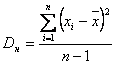Состоятельная и несмещенная оценка СКО результатов наблюдений определится из выражения:

,

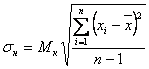где  - коэффициент, зависящий от числа наблюдений. При числе наблюдений меньшем  60 значение больше 1 и определяется из таблиц.

Оценка СКО результата измерения определяется по формуле:

 

.

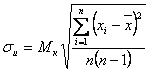Точечные оценки результатов наблюдений необходимы прежде всего для того, чтобы записать результат измерения в виде

,

где - доверительный интервал, в который попадает значение измеряемой величины  при заданном уровне значимости  .

Доверительный интервал определяется из выражения:

,

где  - коэффициент Стьюдента, определяемый из таблиц по числу наблюдений n  и уровню значимости .

Предыдущая | Главная | Глава 7 | Следующая