Предыдущая | Главная | Глава 2 | Следующая 2


2.3. Операции над множествами

 

          Можно производить новые множества путем применения к исходным множествам определенных операций. Изучение операций над множествами составляет предмет алгебры множеств, имеющей много общего с обыкновенной алгеброй чисел, но и отличающейся от нее в некоторых случаях.

         Рассмотрим операции, которые выполняются над множествами.                 

2.3.1. Объединение множеств

         Объединением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т. е. принадлежат А, или принадлежат В, или принадлежат и А и В. Объединение множеств А и В обозначается через АÈВ. Таким образом,

С=АÈВ={cïcÎA  или сÎВ}.

         Напомним, что согласно «определению» множества, если один и тот же элемент содержится и в множестве А и в множестве В, то в их объединение этот элемент включается только один раз.

         Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АÈВ={1, 2, 3, 4, 5, 6, 7}. Если А – множество отличников группы, а В – множество хорошистов, то АÈВ составляет множество и отличников, и хорошистов. Если А – множество отличников группы, а В – все множество студентов группы, то элементами АÈВ являются все студенты группы.

         По аналогии с алгеброй чисел объединение иногда называют суммой множеств.

Операции с множествами удобно иллюстрировать при помощи графических схем, в которых отдельные множества представляются в виде кругов. Предполагается, что элементами множества являются все точки круга. Такие круги называются диаграммами Вена или кругами Эйлера.

         Если А – множество точек левого круга, а В – точек правого круга на рис.2.1, то заштрихованная фигура есть АÈВ.

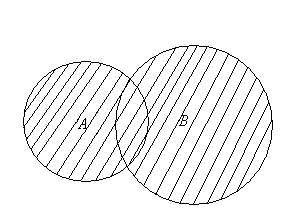
Рис. 2.1

 

         Операция «объединение» аналогичным образом распространяется и для трех, четырех и вообще n множеств , , …, . Множество С=ÈÈ…È –  это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств , , …, .

         Например, если А – множество успевающих студентов группы, В – множество юношей, а С – множество неуспевающих девушек, то АÈВÈС - множество всех студентов группы.

Из определения операции объединение следует, что она обладает многими теми же свойствами, что и операция сложения чисел:

          АÈВ = ВÈА  –  коммутативность (переместительность);

         (АÈВ)ÈС = АÈ(ВÈС)  –  ассоциативность (сочетательность).

         Однако объединение множеств обладает и такими свойствами, которыми не обладает сложение чисел:

        АÈА = А      –  закон  идемпотентности;

        если АÍВ, то АÈВ = В.

        Например, если А={2, 4}, а В={1, 2, 3, 4, 5}, то АÈВ={1, 2, 3, 4, 5}. Если А – множество успевающих студентов группы, В – множество успевающих юношей, то АÈВ – по прежнему множество успевающих студентов.

2.3.2. Пересечение множеств

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству В одновременно. Объединение множеств А и В обозначается через АÇВ. Таким образом,

С=АÇВ={cïcÎA  и  сÎВ}.

         Т.е. пересечение множеств есть общая часть данных множеств.

          Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – множество юношей, то АÇВ составляет множество юношей-отличников.

По аналогии с алгеброй чисел пересечение называют произведением множеств.

          С помощью кругов Эйлера пересечение множеств А и В изображается следующим образом (заштрихованная часть на рис. 2.2.).

Рис. 2.2

 

          Операцию «пересечение» можно аналогичным образом распространить и на n множеств , , …, . Множество С=ÇÇ…Ç –  это множество, состоящее из элементов, которые принадлежат одновременно всем множествам , , …, .

Можно увидеть использование операции пересечения множеств и при расследовании преступлений. Так, в рассказе Артура Конан Дойла «Пять апельсиновых зернышек» знаменитому сыщику Шерлоку Холмсу необходимо было выяснить автора писем, отправленных в разное время из трех разных портовых городов: Пондишере, Данди и Лондона. Интервалы между отсылкой писем были такими, что добраться из города в город отправитель мог только на корабле. Шерлок Холмс определил пересечение трех множеств: множества парусников, бывших в определенное время в Пондишере, множества парусников, заходивших в Данди, и множества парусников, находящихся в Лондоне. Оказалось, что только одно судно входило во все эти три множества: парусник «Одинокая звезда». Таким образом преступление было раскрыто.

 

          Рассмотрим такой пример. Если А – множество отличников группы, а В – множество неуспевающих студентов, то АÇВ  – пустое множество.

          Если АÇВ=Æ, то множества А и В называются непересекающимися (Рис. 2.3).

Рис. 2.3

 

         В противном случае, т.е. если АÇВ¹Æ, множества А и В пересекаются.

        Операция пересечения множеств обладает многими свойствами операция умножения чисел:

        АÇВ =  ВÇА  –  коммутативность (переместительность);

        (АÇВ)ÇС = АÇ(ВÇС)  –  ассоциативность (сочетательность);

        (АÈВ) ÇС = (АÇС) È (ВÇС)  – дистрибутивность (распределительность).

         Укажем такие свойства операции пересечения множеств, которыми операция умножения чисел не обладает:

        АÇА=А       –   идемпотентность;

        Если АÍВ, то АÇВ=А. Например, если А={2, 4}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – все множество студентов группы, то АÇВ  –   множество отличников группы. Данная ситуация представлена на рис.2.4. с помощью кругов Эйлера.

Рис. 2.4

 

2.3.3. Разность множеств

           В отличие от объединения и пересечения множеств эта операция определяется только для двух множеств. Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В. Разность множеств А и В обозначается через А\В. Таким образом,

С=А\В={cïcÎA  и  сÏВ}.

           Например, если А={1, 2, 3, 4, 5}, а В={2, 4}, то А\В={1, 3, 5}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников.

           С помощью кругов Эйлера для случаев, изображенных на рис.2.5, разность множеств А и В изображается следующим образом (заштрихованная часть).

 

Рис. 2.5

 

           Заметим, что разность множеств не является ни коммутативной, ни ассоциативной операцией.

2.3.4. Симметрическая разность множеств

           Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств А или В. Симметрическая разность множеств А и В обозначается через АDВ.

С=АDВ= (А\В)È (В\А).

           Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АDВ={1, 3, 5, 6, 7}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников и юношей-неотличников.

           С помощью кругов Эйлера симметрическая  разность множеств А и В АDВ изображается следующим образом (заштрихованная часть на рис. 2.6).

Рис. 2.6

 

           В отличие от разности множеств симметрическая разность является коммутативной, ассоциативной и дистрибутивной операцией:

          АDВ =  ВDА  –  коммутативность (переместительность);

         (АDВ)DС = АD(ВDС)  –  ассоциативность (сочетательность);

         (АDВ)ÇС = (АÇС) D (ВÇС)  – дистрибутивность (распределительность).

        

         Пример 2.1. Найти АÈВ, АÇВ,  А\В, В\А, АDВ, если А=[1, 3), а B=(2, 4].

         Изобразим множества А и В на числовой прямой.

Рис. 2.7

         Напомним, что если точка не входит во множество она обозначается «белой», если принадлежит множеству – «черной». Множество А обозначено штриховкой с наклоном вправо, множество В – штриховкой с наклоном влево.

         Из рисунка видно, что объединением множеств А и В является множество АÈВ=[1, 4], пересечением множеств А и В – множество АÇВ=(2, 3). Разность  множеств А\В=[1, 2]. (По определению это элементы множества А, исключая элементы множества В. Число 2 не входит в множество В, поэтому оно включается в А\В.)  Аналогично, В\А=[3, 4]. Симметрическая разность АDВ получается путем объединения множеств А\В и В\А: АDВ=[1, 2] È [3, 4].

         Пример 2.2. Даны множества А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, С={6, 7, 8, 9}. Найти множество (АÈВ) D (ВÈС).

         Сначала найдем множества, стоящие в скобках АÈВ={1, 2, 3, 4, 5, 6, 7}, ВÈС={2, 4, 6, 7, 8, 9}. Теперь вычтем из первого множества второе и из второго первое: (АÈВ)\(ВÈС)={1, 3, 5}, (ВÈС)\(АÈВ)= {8, 9}. Объединяя эти множества, получаем (АÈВ) D (ВÈС)={1, 3, 5, 8, 9}.

          Достаточно часто круги Эйлера применяются для наглядного представления и последующего упрощения некоторого сложного выражения или совокупности условий на несколько множеств.

Пример 2.3. Заштрихуйте ту часть диаграммы, которая соответствует множеству (АÇВ)\С, для случая на рис. 2.8.

Рис. 2.8

         Построение кругов Эйлера для сложного выражения, составленного для нескольких множеств посредством операций над ними, осуществляется комбинированием описанных способов построения для этих составных частей. Сначала изобразим пересечение множеств А и В (рис. 2.9.а)). А затем вычтем из (АÇВ) множество С (рис. 2.9.b)).

                     

                         a) АÇВ                                                              b) (АÇВ)\С

Рис. 2.9

           Пример 2.4. Пусть А и В такие множества, что А\В=В\А=Æ. Записать отношение между множествами А и В более простым способом.

           Выражение А\В=Æ означает, что во множестве А нет элементов, которые не принадлежали бы В. Значит все элементы А принадлежат В. Это означает, что АÍВ (рис.2.10.а)). Аналогично, из выражения В\А=Æ следует, что ВÍА. Т.е. АÍВ и ВÍА (рис.2.10.b)).

                             

                a) АÍВ                                                               b) ВÍА                  

Рис. 2.10

           Таким образом, согласно свойству включений (2.3) А=В.

Предыдущая | Главная | Глава 2 | Следующая