5.6. Геометрическое и статистическое определения вероятности

 

Иногда недостаток конечного числа возможных исходов испытания можно преодолеть, используя геометрическое определение вероятности.

Рассмотрим некоторую замкнутую область G в пространстве (рис.5.1). Обозначим через  ее меру. Если  область – одномерная (отрезок), то мерой будет ее длина, если область двумерная (некоторая плоская фигура), то ее мера - площадь, если трехмерная (тело в пространстве), то – объем. Пусть область D полностью содержится в области G. Мера области D - .

Рассмотрим следующий эксперимент: случайно из области G выбирается точка А.  Необходимо определить вероятность попадания точки А в подобласть D.

Роль элементарных событий в данном эксперименте играют точки области G. Все множество точек области G образует пространство элементарных событий. Все элементарные события – равновозможны, так как все точки области G равноправны в отношении попадания туда случайной точки A. Но число этих элементарных событий бесконечно. Поэтому в данном случае классическое определение вероятности не применимо.

Согласно геометрическому определению,

вероятность  случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е.

.

         Пример 5.17. Задача о встрече. Двое лиц договариваются о встрече на следующих условиях: каждый из них приходит к указанному месту независимо друг от друга в любой момент времени от двенадцати до часу и ждет другого в течение 20 минут, после чего уходит. Какова вероятность того, что встреча состоится?

         Решение. Обозначим через x и y моменты прихода к месту встречи 1-го и 2-го лица. Изобразим момент встречи в декартовой системе координат Oxy: за начало координат возьмем 12 ч., а за единицу измерения – 1ч. Элементарное событие исхода встречи – упорядоченная пара чисел (x, y) – обозначается на плоскости точкой. Так как по условию задачи встречающиеся должны прийти к назначенному месту в течение часа, то ,  и множество всех элементарных событий G образует на плоскости квадрат со стороной 1. =1.

         Встреча произойдет тогда и только тогда, если разность между x и y будет меньше либо равна ч., т.е. если . Этим неравенством и определяется подобласть D.

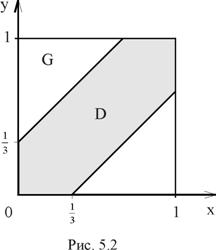
Изобразим на графике (рис.5.2) границы подобласти D: y - x =  и  y - x=;  y= x+  и  y= x.

 

Найдем площадь области D.

=.

         По геометрическому определению вероятность встречи =.

 

Существует большой класс событий, которые могут появиться в результате испытаний, не обладающих симметрией возможных исходов. Так, например, из соображений симметрии невозможно определить вероятность раскрытия какого-либо типа преступления конкретным следователем или вероятность рождения определенного количества мальчиков в год. В этих случаях вероятность случайного события можно определить исходя из того, насколько часто данное событие будет появляться в однотипных испытаниях.

Если производится серия из n испытаний, в каждом из которых может появиться (или не появиться) случайное событие А, то отношение числа испытаний, в которых появилось событие А - m, к общему числу испытаний n называют статистической вероятностью события А в данной серии испытаний .

Итак, статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е.

,

где m – число испытаний, в которых появилось событие А; 

n – общее число испытаний.

         Это и есть статистическое определение вероятности.

 

         В отличие от вероятности , рассматриваемой в классическом определении, статистическая вероятность  - величина опытная, полученная в результате эксперимента.  в значительной мере имеет случайный характер.

Рассмотрим испытание, состоящее в бросании плоской монеты, и событие А – выпадение герба. Классическая вероятность этого события . Что касается статистической вероятности события , то она зависит от числа произведенных испытаний в серии и может не равняться 0,5. Скажем, если общее число испытаний n будет нечетным, то число выпавших гербов всегда будет не равно числу «решек» и  будет отличаться от 0,5. Однако для дальнейшего использования статистической вероятности важно насколько она отличается от полученной из классического определения. Произведем серию из 60 испытаний, каждый раз подсчитывая статистическую вероятность выпадения герба. 

 

Появление герба - 1, решки - 0	Число выпавших гербов	Число испыта-ний	Статистическая вероятность	Появление герба - 1, решки - 0	Число выпавших гербов	Число испытаний	Статистическая вероятность
1	1	1	1,0000	0	16	31	0,5161
0	1	2	0,5000	0	16	32	0,5000
1	2	3	0,6667	0	16	33	0,4848
1	3	4	0,7500	1	17	34	0,5000
0	3	5	0,6000	1	18	35	0,5143
0	3	6	0,5000	0	18	36	0,5000
1	4	7	0,5714	1	19	37	0,5135
1	5	8	0,6250	0	19	38	0,5000
0	5	9	0,5556	1	20	39	0,5128
1	6	10	0,6000	0	20	40	0,5000
1	7	11	0,6364	1	21	41	0,5122
0	7	12	0,5833	1	22	42	0,5238
1	8	13	0,6154	0	22	43	0,5116
0	8	14	0,5714	0	22	44	0,5000
0	8	15	0,5333	1	23	45	0,5111
1	9	16	0,5625	1	24	46	0,5217
0	9	17	0,5294	0	24	47	0,5106
0	9	18	0,5000	1	25	48	0,5208
1	10	19	0,5263	0	25	49	0,5102
1	11	20	0,5500	0	25	50	0,5000
0	11	21	0,5238	1	26	51	0,5098
0	11	22	0,5000	0	26	52	0,5000
1	12	23	0,5217	1	27	53	0,5094
1	13	24	0,5417	0	27	54	0,5000
0	13	25	0,5200	0	27	55	0,4909
0	13	26	0,5000	1	28	56	0,5000
1	14	27	0,5185	1	29	57	0,5088
0	14	28	0,5000	0	29	58	0,5000
1	15	29	0,5172	0	29	59	0,4915
1	16	30	0,5333	1	30	60	0,5000

 

Если количество произведенных испытаний n мало, например, произведено три бросания, то герб может не появиться один раз, т.е., вообще ни разу -  или все три раза . Т.о. статистическая вероятность не будет совпадать со значением, полученным из классического определения, и будет вести себя случайным образом. Из таблицы видно, что при небольшом числе опытов (n<10) относительная частота выпадения герба заметно отличается от классической вероятности. При n=10 =0,60; при n=20 =0,55; при n=30 =0,5333. При очень большом числе опытов статистическая частота выпадения герба приближается к значению классической вероятности 0,5, колеблясь вокруг этой величины. Причем, чем больше n, тем меньше разность -0,5. Колебания частоты около этого значения носят случайный характер.

 

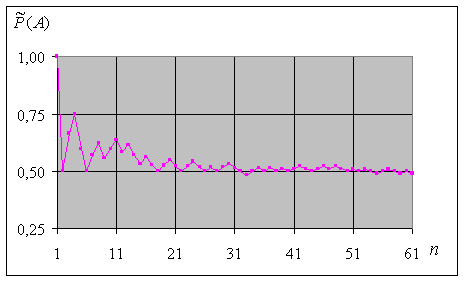
Рис.5.3

 

На рис.5.3 приведен график зависимости относительной частоты появления герба при бросании монеты  от числа опытов n. Из графика видно, что по мере увеличения n частота стабилизируется, стремясь к постоянной величине, которую мы полагаем равной 0,5. Это значение и есть вероятность выпадения герба в одном опыте, подсчитанная при помощи классического определения.

На данном примере, сводящемся к схеме случаев, мы показали, что при достаточно большом количестве опытов относительную частоту события можно принять за приближенное значение его вероятности. Естественно допустить, что и для опытов, не сводящихся к схеме случаев, постоянное значение, к которому при увеличении числа испытаний приближается относительная частота события и есть вероятность этого события.

Здесь возникает вопрос: к любым ли событиям с неопределенным исходом, которые в житейской практике считаются случайными, применимо статистическое определение вероятности? Оказывается, для расчета вероятности по статистическому определению необходимо, чтобы случайное событие обладало рядом свойств.

1.    Рассматриваемые события должны быть исходами испытания, которые можно повторить неограниченное число раз. Напомним, что испытание мы определили как совокупность условий, при которых происходит или не происходит случайное событие. Таким образом, для использования статистического определения необходимо, чтобы комплекс условий, при которых реализуется случайное событие, был идентичен и его можно было повторить неограниченное число раз. Поэтому бессмысленно ставить вопрос об определении вероятности, например, возникновения войны или совершения преступления, поскольку данные события возникают при уникальных, неповторимых условиях.

2.    Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.

3.    События должны обладать статистической устойчивостью. Это означает, что в различных сериях испытаний относительная частота должна изменяться незначительно, колеблясь около постоянного числа. Это число и является вероятностью случайного события.

 

Предыдущая | Главная | Глава 5 | Следующая